Chi-Square One-Sample Goodness-of-Fit Tests

11.2 Chi-Square One-Sample Goodness-of-Fit Tests

Learning Objective

To understand how to use a chi-square test to judge whether a sample fits a particular population well.

Suppose we wish to determine if an ordinary-looking six-sided die is fair, or balanced, meaning that every face has probability 1/6 of landing on top when the die is tossed. We could toss the die dozens, maybe hundreds, of times and compare the actual number of times each face landed on top to the expected number, which would be 1/6 of the total number of tosses. We wouldn’t expect each number to be exactly 1/6 of the total, but it should be close. To be specific, suppose the die is tossed n = 60 times with the results summarized in Table 11.8 "Die Contingency Table". For ease of reference we add a column of expected frequencies, which in this simple example is simply a column of 10s. The result is shown as Table 11.9 "Updated Die Contingency Table". In analogy with the previous section we call this an “updated” table. A measure of how much the data deviate from what we would expect to see if the die really were fair is the sum of the squares of the differences between the observed frequency O and the expected frequency E in each row, or, standardizing by dividing each square by the expected number, the sum $Σ {(O - E)}^{2} ∕ E .$ If we formulate the investigation as a test of hypotheses, the test is

\begin{matrix} H_{0} & : & The die is fair \\ vs. H_{a} & : & The die is n o t fair \end{matrix}

Table 11.8 Die Contingency Table

Die Value	Assumed Distribution	Observed Frequency
1	1/6	9
2	1/6	15
3	1/6	9
4	1/6	8
5	1/6	6
6	1/6	13

Table 11.9 Updated Die Contingency Table

Die Value	Assumed Distribution	Observed Freq.	Expected Freq.
1	1/6	9	10
2	1/6	15	10
3	1/6	9	10
4	1/6	8	10
5	1/6	6	10
6	1/6	13	10

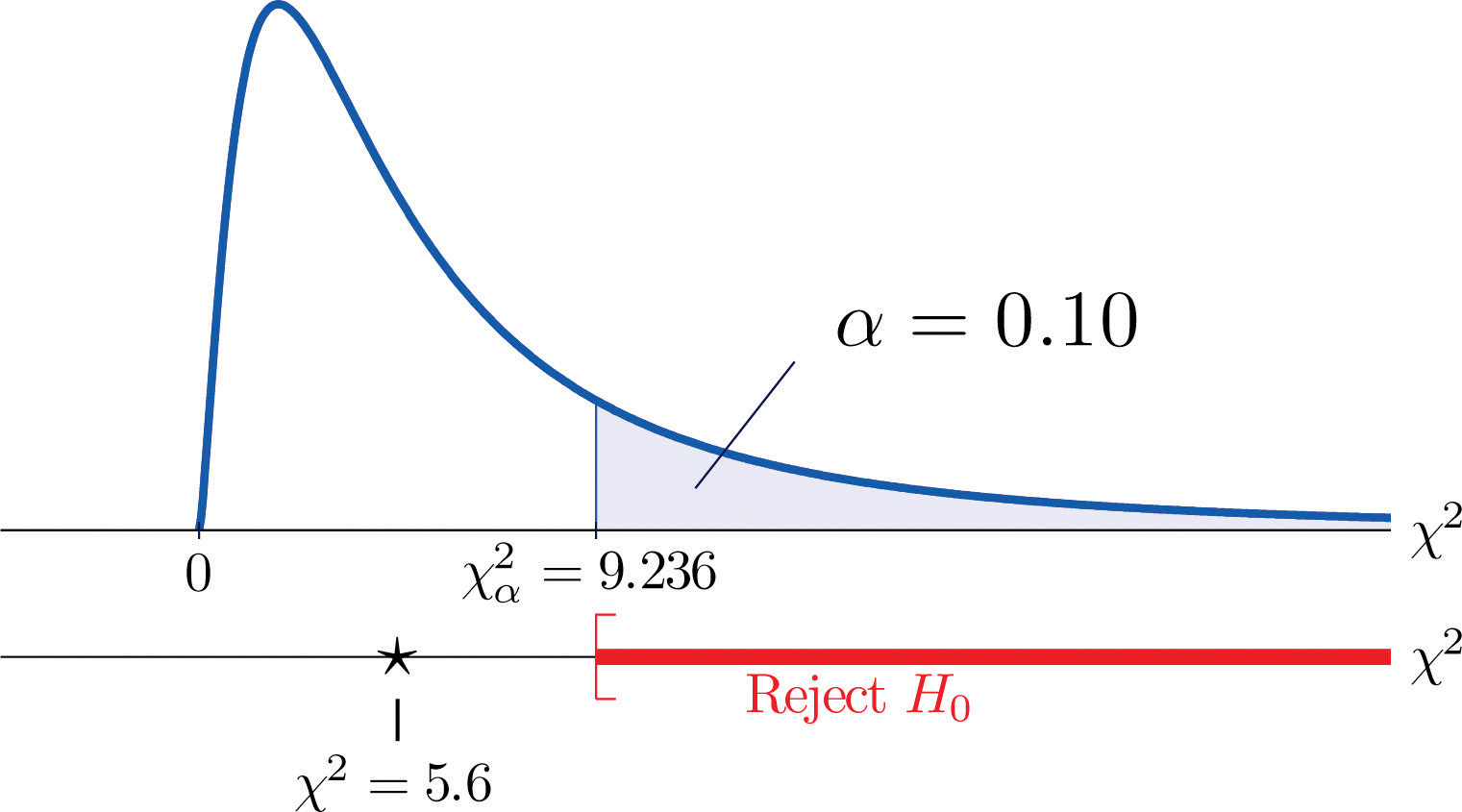
We would reject the null hypothesis that the die is fair only if the number $Σ {(O - E)}^{2} ∕ E$ is large, so the test is right-tailed. In this example the random variable $Σ {(O - E)}^{2} ∕ E$ has the chi-square distribution with five degrees of freedom. If we had decided at the outset to test at the 10% level of significance, the critical value defining the rejection region would be, reading from Figure 12.4 "Critical Values of Chi-Square Distributions", $χ_{α}^{2} = χ_{0.10}^{2} = 9.236$ , so that the rejection region would be the interval $[9.236, \infty) .$ When we compute the value of the standardized test statistic using the numbers in the last two columns of Table 11.9 "Updated Die Contingency Table", we obtain

\begin{matrix} Σ \frac{{(O - E)}^{2}}{E} \\ = \frac{{(− 1)}^{2}}{10} + \frac{5^{2}}{10} + \frac{{(− 1)}^{2}}{10} + \frac{{(− 2)}^{2}}{10} + \frac{{(− 4)}^{2}}{10} + \frac{3^{2}}{10} \\ = 0.1 + 2.5 + 0.1 + 0.4 + 1.6 + 0.9 \\ = 5.6 \end{matrix}

Since 5.6 < 9.236 the decision is not to reject H₀. See Figure 11.5 "Balanced Die". The data do not provide sufficient evidence, at the 10% level of significance, to conclude that the die is loaded.

Figure 11.5 Balanced Die

In the general situation we consider a discrete random variable that can take I different values, $x_{1}, x_{2}, \dots, x_{I}$ , for which the default assumption is that the probability distribution is

\begin{matrix} x & x_{1} & x_{2} & \dots & x_{I} \\ P (x) & p_{1} & p_{2} & \dots & p_{I} \end{matrix}

We wish to test the hypotheses

\begin{matrix} H_{0} & : & The assumed probability distribution for X is valid \\ vs. H_{a} & : & The assumed probability distribution for X is n o t valid \end{matrix}

We take a sample of size n and obtain a list of observed frequencies. This is shown in Table 11.10 "General Contingency Table". Based on the assumed probability distribution we also have a list of assumed frequencies, each of which is defined and computed by the formula

E_{i} = n \times p_{i}

Table 11.10 General Contingency Table

Factor Levels	Assumed Distribution	Observed Frequency
1	p₁	O₁
2	p₂	O₂
⋮	⋮	⋮
I	p_I	O_I

Table 11.10 "General Contingency Table" is updated to Table 11.11 "Updated General Contingency Table" by adding the expected frequency for each value of X. To simplify the notation we drop indices for the observed and expected frequencies and represent Table 11.11 "Updated General Contingency Table" by Table 11.12 "Simplified Updated General Contingency Table".

Table 11.11 Updated General Contingency Table

Factor Levels	Assumed Distribution	Observed Freq.	Expected Freq.
1	p₁	O₁	E₁
2	p₂	O₂	E₂
⋮	⋮	⋮	⋮
I	p_I	O_I	E_I

Table 11.12 Simplified Updated General Contingency Table

Factor Levels	Assumed Distribution	Observed Freq.	Expected Freq.
1	p₁	O	E
2	p₂	O	E
⋮	⋮	⋮	⋮
I	p_I	O	E

Here is the test statistic for the general hypothesis based on Table 11.12 "Simplified Updated General Contingency Table", together with the conditions that it follow a chi-square distribution.

Test Statistic for Testing Goodness of Fit to a Discrete Probability Distribution

χ^{2} = Σ \frac{{(O - E)}^{2}}{E}

where the sum is over all the rows of the table (one for each value of X).

the true probability distribution of X is as assumed, and
the observed count O of each cell in Table 11.12 "Simplified Updated General Contingency Table" is at least 5,

then $χ^{2}$ approximately follows a chi-square distribution with $d f = I − 1$ degrees of freedom.

The test is known as a goodness-of-fit $χ^{2}$ test since it tests the null hypothesis that the sample fits the assumed probability distribution well. It is always right-tailed, since deviation from the assumed probability distribution corresponds to large values of $χ^{2} .$

Testing is done using either of the usual five-step procedures.

Example 2

Table 11.13 "Ethnic Groups in the Census Year" shows the distribution of various ethnic groups in the population of a particular state based on a decennial U.S. census. Five years later a random sample of 2,500 residents of the state was taken, with the results given in Table 11.14 "Sample Data Five Years After the Census Year" (along with the probability distribution from the census year). Test, at the 1% level of significance, whether there is sufficient evidence in the sample to conclude that the distribution of ethnic groups in this state five years after the census had changed from that in the census year.

Table 11.13 Ethnic Groups in the Census Year

Ethnicity	White	Black	Amer.-Indian	Hispanic	Asian	Others
Proportion	0.743	0.216	0.012	0.012	0.008	0.009

Table 11.14 Sample Data Five Years After the Census Year

Ethnicity	Assumed Distribution	Observed Frequency
White	0.743	1732
Black	0.216	538
American-Indian	0.012	32
Hispanic	0.012	42
Asian	0.008	133
Others	0.009	23

Solution:

We test using the critical value approach.

Step 1. The hypotheses of interest in this case can be expressed as
$\begin{matrix} H_{0} & : & The distribution of ethnic groups has not changed \\ vs. H_{a} & : & The distribution of ethnic groups h a s changed \end{matrix}$
Step 2. The distribution is chi-square.

Step 3. To compute the value of the test statistic we must first compute the expected number for each row of Table 11.14 "Sample Data Five Years After the Census Year". Since n = 2500, using the formula $E_{i} = n \times p_{i}$ and the values of p_i from either Table 11.13 "Ethnic Groups in the Census Year" or Table 11.14 "Sample Data Five Years After the Census Year",

\begin{matrix} E_{1} & = & 2500 \times 0.743 = 1857.5 \\ E_{2} & = & 2500 \times 0.216 = 540 \\ E_{3} & = & 2500 \times 0.012 = 30 \\ E_{4} & = & 2500 \times 0.012 = 30 \\ E_{5} & = & 2500 \times 0.008 = 20 \\ E_{6} & = & 2500 \times 0.009 = 22.5 \end{matrix}

Table 11.14 "Sample Data Five Years After the Census Year" is updated to Table 11.15 "Observed and Expected Frequencies Five Years After the Census Year".

Table 11.15 Observed and Expected Frequencies Five Years After the Census Year

Ethnicity	Assumed Dist.	Observed Freq.	Expected Freq.
White	0.743	1732	1857.5
Black	0.216	538	540
American-Indian	0.012	32	30
Hispanic	0.012	42	30
Asian	0.008	133	20
Others	0.009	23	22.5

The value of the test statistic is

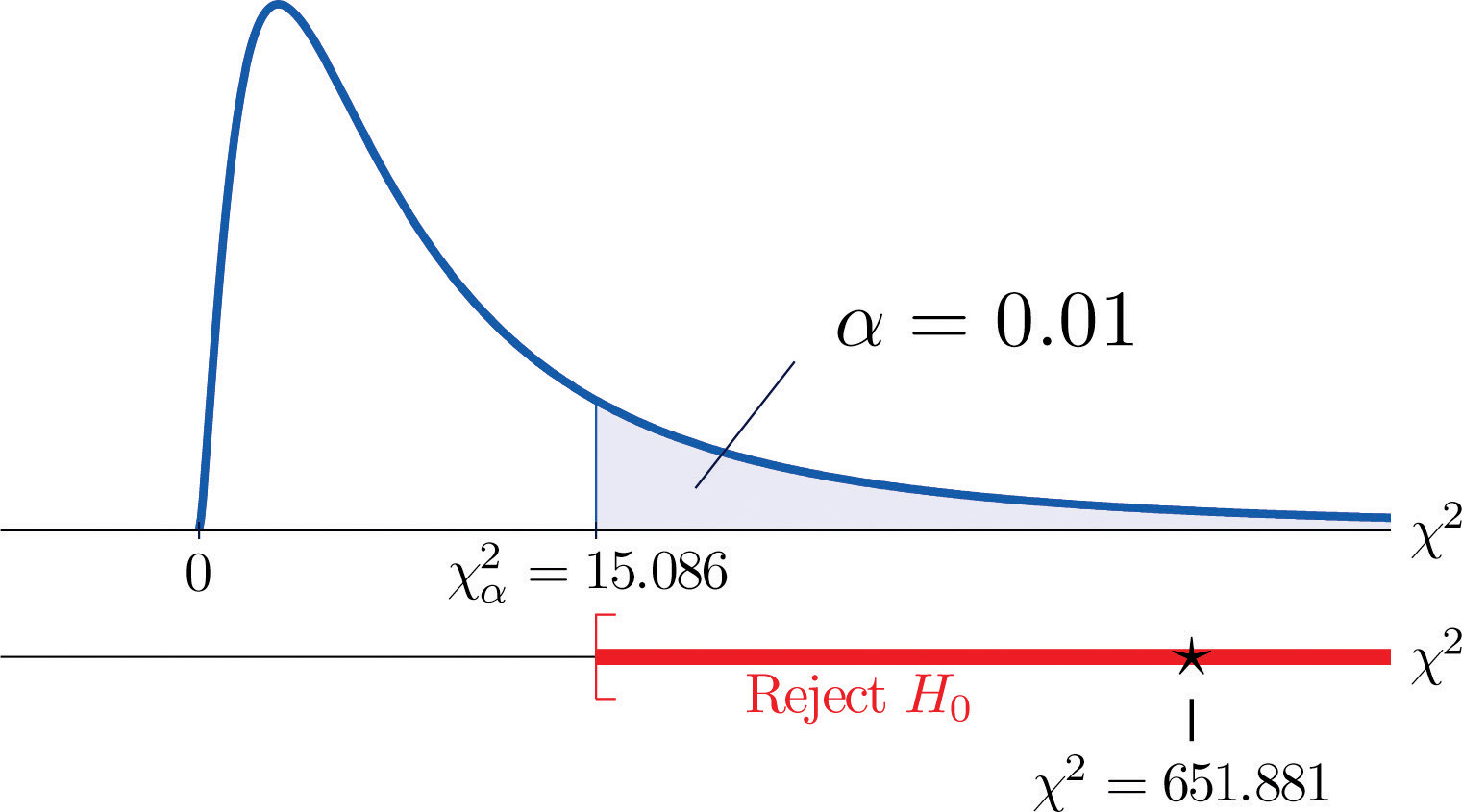
\begin{matrix} χ^{2} & = & Σ \frac{{(O - E)}^{2}}{E} \\ = & \frac{{(1732 - 1857.5)}^{2}}{1857.5} + \frac{{(538 - 540)}^{2}}{540} + \frac{{(32 - 30)}^{2}}{30} + \frac{{(42 - 30)}^{2}}{30} \\ + \frac{{(133 - 20)}^{2}}{20} + \frac{{(23 - 22.5)}^{2}}{22.5} \\ = & 651.881 \end{matrix}

Since the random variable takes six values, I = 6. Thus the test statistic follows the chi-square distribution with $d f = 6 - 1 = 5$ degrees of freedom.

Since the test is right-tailed, the critical value is $χ_{0.01}^{2} .$ Reading from Figure 12.4 "Critical Values of Chi-Square Distributions", $χ_{0.01}^{2} = 15.086$ , so the rejection region is $[15.086, \infty) .$
Since 651.881 > 15.086 the decision is to reject the null hypothesis. See Figure 11.6. The data provide sufficient evidence, at the 1% level of significance, to conclude that the ethnic distribution in this state has changed in the five years since the U.S. census.

Figure 11.6 Note 11.15 "Example 2"

Key Takeaway

The chi-square goodness-of-fit testA test based on a chi-square statistic to check whether a sample is taken from a population with a hypothesized probability distribution. can be used to evaluate the hypothesis that a sample is taken from a population with an assumed specific probability distribution.

Exercises

Basic

A data sample is sorted into five categories with an assumed probability distribution.

Factor Levels Assumed Distribution Observed Frequency

1 $p_{1} = 0.1$ 10

2 $p_{2} = 0.4$ 35

3 $p_{3} = 0.4$ 45

4 $p_{4} = 0.1$ 10
1. Find the size n of the sample.
2. Find the expected number E of observations for each level, if the sampled population has a probability distribution as assumed (that is, just use the formula $E_{i} = n \times p_{i}$ ).
3. Find the chi-square test statistic $χ^{2} .$
4. Find the number of degrees of freedom of the chi-square test statistic.
A data sample is sorted into five categories with an assumed probability distribution.

Factor Levels Assumed Distribution Observed Frequency

1 $p_{1} = 0.3$ 23

2 $p_{2} = 0.3$ 30

3 $p_{3} = 0.2$ 19

4 $p_{4} = 0.1$ 8

5 $p_{5} = 0.1$ 10
1. Find the size n of the sample.
2. Find the expected number E of observations for each level, if the sampled population has a probability distribution as assumed (that is, just use the formula $E_{i} = n \times p_{i}$ ).
3. Find the chi-square test statistic $χ^{2} .$
4. Find the number of degrees of freedom of the chi-square test statistic.

Factor Levels	Assumed Distribution	Observed Frequency
1	$p_{1} = 0.1$	10
2	$p_{2} = 0.4$	35
3	$p_{3} = 0.4$	45
4	$p_{4} = 0.1$	10

Factor Levels	Assumed Distribution	Observed Frequency
1	$p_{1} = 0.3$	23
2	$p_{2} = 0.3$	30
3	$p_{3} = 0.2$	19
4	$p_{4} = 0.1$	8
5	$p_{5} = 0.1$	10

Applications

Retailers of collectible postage stamps often buy their stamps in large quantities by weight at auctions. The prices the retailers are willing to pay depend on how old the postage stamps are. Many collectible postage stamps at auctions are described by the proportions of stamps issued at various periods in the past. Generally the older the stamps the higher the value. At one particular auction, a lot of collectible stamps is advertised to have the age distribution given in the table provided. A retail buyer took a sample of 73 stamps from the lot and sorted them by age. The results are given in the table provided. Test, at the 5% level of significance, whether there is sufficient evidence in the data to conclude that the age distribution of the lot is different from what was claimed by the seller.

Year Claimed Distribution Observed Frequency

Before 1940 0.10 6

1940 to 1959 0.25 15

1960 to 1979 0.45 30

After 1979 0.20 22
The litter size of Bengal tigers is typically two or three cubs, but it can vary between one and four. Based on long-term observations, the litter size of Bengal tigers in the wild has the distribution given in the table provided. A zoologist believes that Bengal tigers in captivity tend to have different (possibly smaller) litter sizes from those in the wild. To verify this belief, the zoologist searched all data sources and found 316 litter size records of Bengal tigers in captivity. The results are given in the table provided. Test, at the 5% level of significance, whether there is sufficient evidence in the data to conclude that the distribution of litter sizes in captivity differs from that in the wild.

Litter Size Wild Litter Distribution Observed Frequency

1 0.11 41

2 0.69 243

3 0.18 27

4 0.02 5

Year	Claimed Distribution	Observed Frequency
Before 1940	0.10	6
1940 to 1959	0.25	15
1960 to 1979	0.45	30
After 1979	0.20	22

Litter Size	Wild Litter Distribution	Observed Frequency
1	0.11	41
2	0.69	243
3	0.18	27
4	0.02	5

An online shoe retailer sells men’s shoes in sizes 8 to 13. In the past orders for the different shoe sizes have followed the distribution given in the table provided. The management believes that recent marketing efforts may have expanded their customer base and, as a result, there may be a shift in the size distribution for future orders. To have a better understanding of its future sales, the shoe seller examined 1,040 sales records of recent orders and noted the sizes of the shoes ordered. The results are given in the table provided. Test, at the 1% level of significance, whether there is sufficient evidence in the data to conclude that the shoe size distribution of future sales will differ from the historic one.

Shoe Size	Past Size Distribution	Recent Size Frequency
8.0	0.03	25
8.5	0.06	43
9.0	0.09	88
9.5	0.19	221
10.0	0.23	272
10.5	0.14	150
11.0	0.10	107
11.5	0.06	51
12.0	0.05	37
12.5	0.03	35
13.0	0.02	11

An online shoe retailer sells women’s shoes in sizes 5 to 10. In the past orders for the different shoe sizes have followed the distribution given in the table provided. The management believes that recent marketing efforts may have expanded their customer base and, as a result, there may be a shift in the size distribution for future orders. To have a better understanding of its future sales, the shoe seller examined 1,174 sales records of recent orders and noted the sizes of the shoes ordered. The results are given in the table provided. Test, at the 1% level of significance, whether there is sufficient evidence in the data to conclude that the shoe size distribution of future sales will differ from the historic one.

Shoe Size	Past Size Distribution	Recent Size Frequency
5.0	0.02	20
5.5	0.03	23
6.0	0.07	88
6.5	0.08	90
7.0	0.20	222
7.5	0.20	258
8.0	0.15	177
8.5	0.11	121
9.0	0.08	91
9.5	0.04	53
10.0	0.02	31

A chess opening is a sequence of moves at the beginning of a chess game. There are many well-studied named openings in chess literature. French Defense is one of the most popular openings for black, although it is considered a relatively weak opening since it gives black probability 0.344 of winning, probability 0.405 of losing, and probability 0.251 of drawing. A chess master believes that he has discovered a new variation of French Defense that may alter the probability distribution of the outcome of the game. In his many Internet chess games in the last two years, he was able to apply the new variation in 77 games. The wins, losses, and draws in the 77 games are given in the table provided. Test, at the 5% level of significance, whether there is sufficient evidence in the data to conclude that the newly discovered variation of French Defense alters the probability distribution of the result of the game.

Result for Black Probability Distribution New Variation Wins

Win 0.344 31

Loss 0.405 25

Draw 0.251 21
The Department of Parks and Wildlife stocks a large lake with fish every six years. It is determined that a healthy diversity of fish in the lake should consist of 10% largemouth bass, 15% smallmouth bass, 10% striped bass, 10% trout, and 20% catfish. Therefore each time the lake is stocked, the fish population in the lake is restored to maintain that particular distribution. Every three years, the department conducts a study to see whether the distribution of the fish in the lake has shifted away from the target proportions. In one particular year, a research group from the department observed a sample of 292 fish from the lake with the results given in the table provided. Test, at the 5% level of significance, whether there is sufficient evidence in the data to conclude that the fish population distribution has shifted since the last stocking.

Fish Target Distribution Fish in Sample

Largemouth Bass 0.10 14

Smallmouth Bass 0.15 49

Striped Bass 0.10 21

Trout 0.10 22

Catfish 0.20 75

Other 0.35 111

Result for Black	Probability Distribution	New Variation Wins
Win	0.344	31
Loss	0.405	25
Draw	0.251	21

Fish	Target Distribution	Fish in Sample
Largemouth Bass	0.10	14
Smallmouth Bass	0.15	49
Striped Bass	0.10	21
Trout	0.10	22
Catfish	0.20	75
Other	0.35	111

Large Data Set Exercise

Large Data Set 4 records the result of 500 tosses of six-sided die. Test, at the 10% level of significance, whether there is sufficient evidence in the data to conclude that the die is not “fair” (or “balanced”), that is, that the probability distribution differs from probability 1/6 for each of the six faces on the die.

https://www.gone.2012books.lardbucket.org/sites/all/files/data4.xls

Answers

1. n = 100,
2. E = 10, E = 40, E = 40, E = 10;
3. $χ^{2} = 1.25$ ,
4. $d f = 3$

$χ^{2} = 4.8082$ , $χ_{0.05}^{2} = 7.81$ , do not reject H₀
$χ^{2} = 26.5765$ , $χ_{0.01}^{2} = 23.21$ , reject H₀
$χ^{2} = 2.1401$ , $χ_{0.05}^{2} = 5.99$ , do not reject H₀

$χ^{2} = 2.944 .$ $d f = 5 .$ Rejection Region: $[9.236, \infty) .$ Decision: Fail to reject H₀ of balance.