You probably have a good intuitive grasp of what the average of a data set says about that data set. In this section we begin to learn what the standard deviation has to tell us about the nature of the data set.
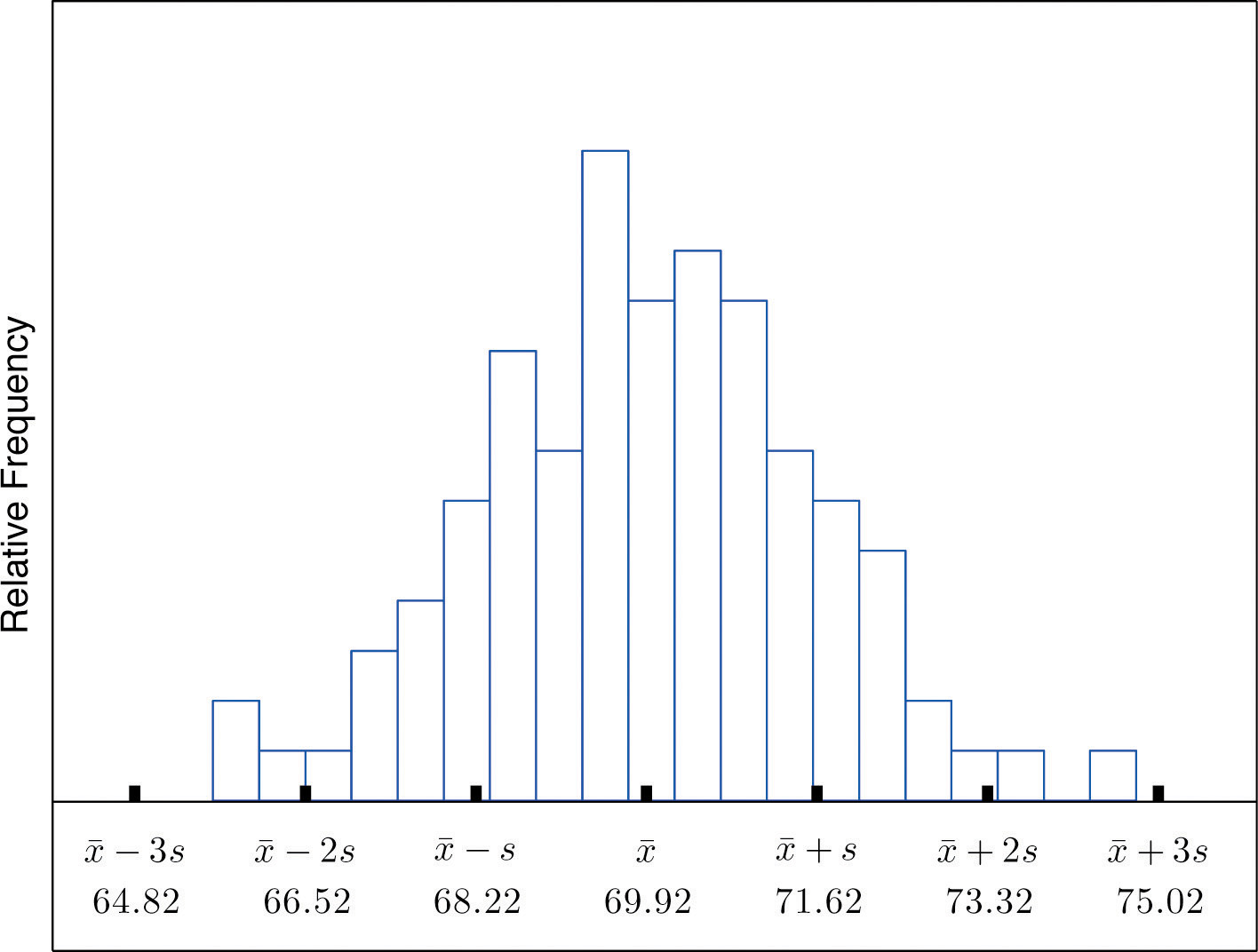
We start by examining a specific set of data. Table 2.2 "Heights of Men" shows the heights in inches of 100 randomly selected adult men. A relative frequency histogram for the data is shown in Figure 2.15 "Heights of Adult Men". The mean and standard deviation of the data are, rounded to two decimal places, ˉx=69.92 and s = 1.70. If we go through the data and count the number of observations that are within one standard deviation of the mean, that is, that are between 69.92−1.70=68.22 and 69.92+1.70=71.62 inches, there are 69 of them. If we count the number of observations that are within two standard deviations of the mean, that is, that are between 69.92−2(1.70)=66.52 and 69.92+2(1.70)=73.32 inches, there are 95 of them. All of the measurements are within three standard deviations of the mean, that is, between 69.92−3(1.70)=64.822 and 69.92+3(1.70)=75.02 inches. These tallies are not coincidences, but are in agreement with the following result that has been found to be widely applicable.
Table 2.2 Heights of Men
| 68.7 | 72.3 | 71.3 | 72.5 | 70.6 | 68.2 | 70.1 | 68.4 | 68.6 | 70.6 |
| 73.7 | 70.5 | 71.0 | 70.9 | 69.3 | 69.4 | 69.7 | 69.1 | 71.5 | 68.6 |
| 70.9 | 70.0 | 70.4 | 68.9 | 69.4 | 69.4 | 69.2 | 70.7 | 70.5 | 69.9 |
| 69.8 | 69.8 | 68.6 | 69.5 | 71.6 | 66.2 | 72.4 | 70.7 | 67.7 | 69.1 |
| 68.8 | 69.3 | 68.9 | 74.8 | 68.0 | 71.2 | 68.3 | 70.2 | 71.9 | 70.4 |
| 71.9 | 72.2 | 70.0 | 68.7 | 67.9 | 71.1 | 69.0 | 70.8 | 67.3 | 71.8 |
| 70.3 | 68.8 | 67.2 | 73.0 | 70.4 | 67.8 | 70.0 | 69.5 | 70.1 | 72.0 |
| 72.2 | 67.6 | 67.0 | 70.3 | 71.2 | 65.6 | 68.1 | 70.8 | 71.4 | 70.2 |
| 70.1 | 67.5 | 71.3 | 71.5 | 71.0 | 69.1 | 69.5 | 71.1 | 66.8 | 71.8 |
| 69.6 | 72.7 | 72.8 | 69.6 | 65.9 | 68.0 | 69.7 | 68.7 | 69.8 | 69.7 |
Figure 2.15 Heights of Adult Men
If a data set has an approximately bell-shaped relative frequency histogram, then (see Figure 2.16 "The Empirical Rule")
Figure 2.16 The Empirical Rule
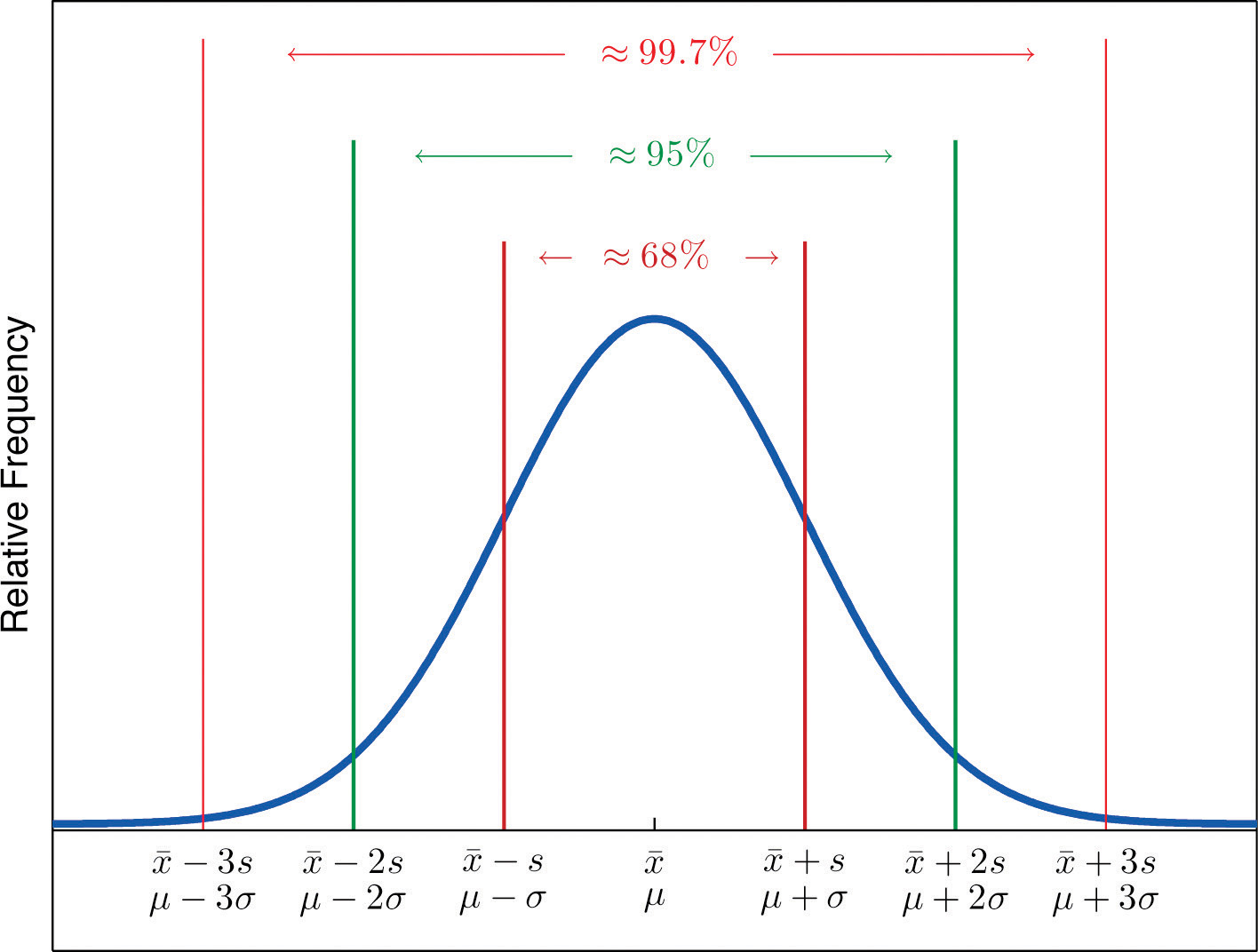
Two key points in regard to the Empirical Rule are that the data distribution must be approximately bell-shaped and that the percentages are only approximately true. The Empirical Rule does not apply to data sets with severely asymmetric distributions, and the actual percentage of observations in any of the intervals specified by the rule could be either greater or less than those given in the rule. We see this with the example of the heights of the men: the Empirical Rule suggested 68 observations between 68.22 and 71.62 inches but we counted 69.
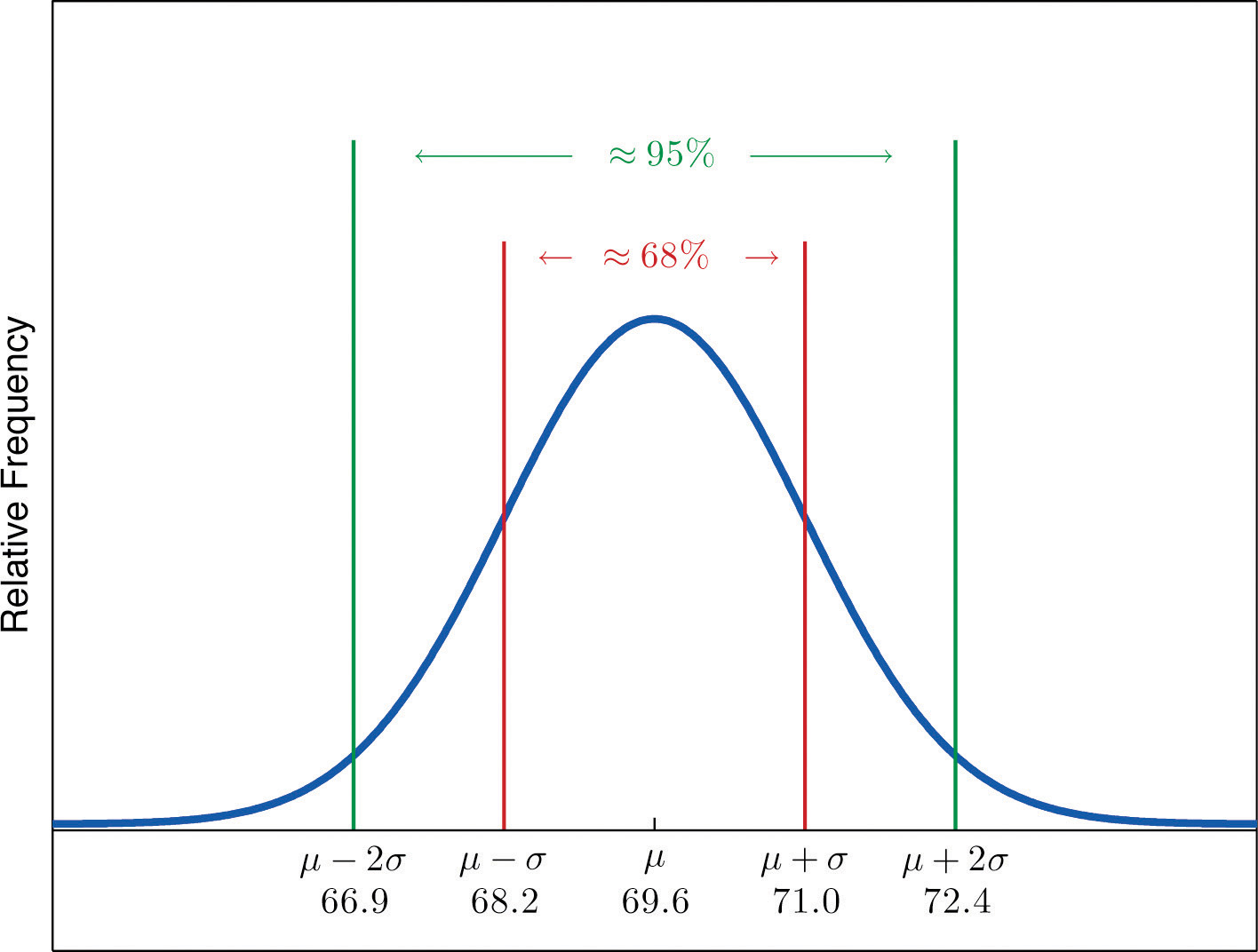
Heights of 18-year-old males have a bell-shaped distribution with mean 69.6 inches and standard deviation 1.4 inches.
Solution:
A sketch of the distribution of heights is given in Figure 2.17 "Distribution of Heights".
By the Empirical Rule the shortest such interval has endpoints ˉx−2s and ˉx+2s. Since
ˉx−2s=69.6−2(1.4)=66.8 and ˉx+2s=69.6+2(1.4)=72.4the interval in question is the interval from 66.8 inches to 72.4 inches.
Figure 2.17 Distribution of Heights
Scores on IQ tests have a bell-shaped distribution with mean μ = 100 and standard deviation σ = 10. Discuss what the Empirical Rule implies concerning individuals with IQ scores of 110, 120, and 130.
Solution:
A sketch of the IQ distribution is given in Figure 2.18 "Distribution of IQ Scores". The Empirical Rule states that
Figure 2.18 Distribution of IQ Scores
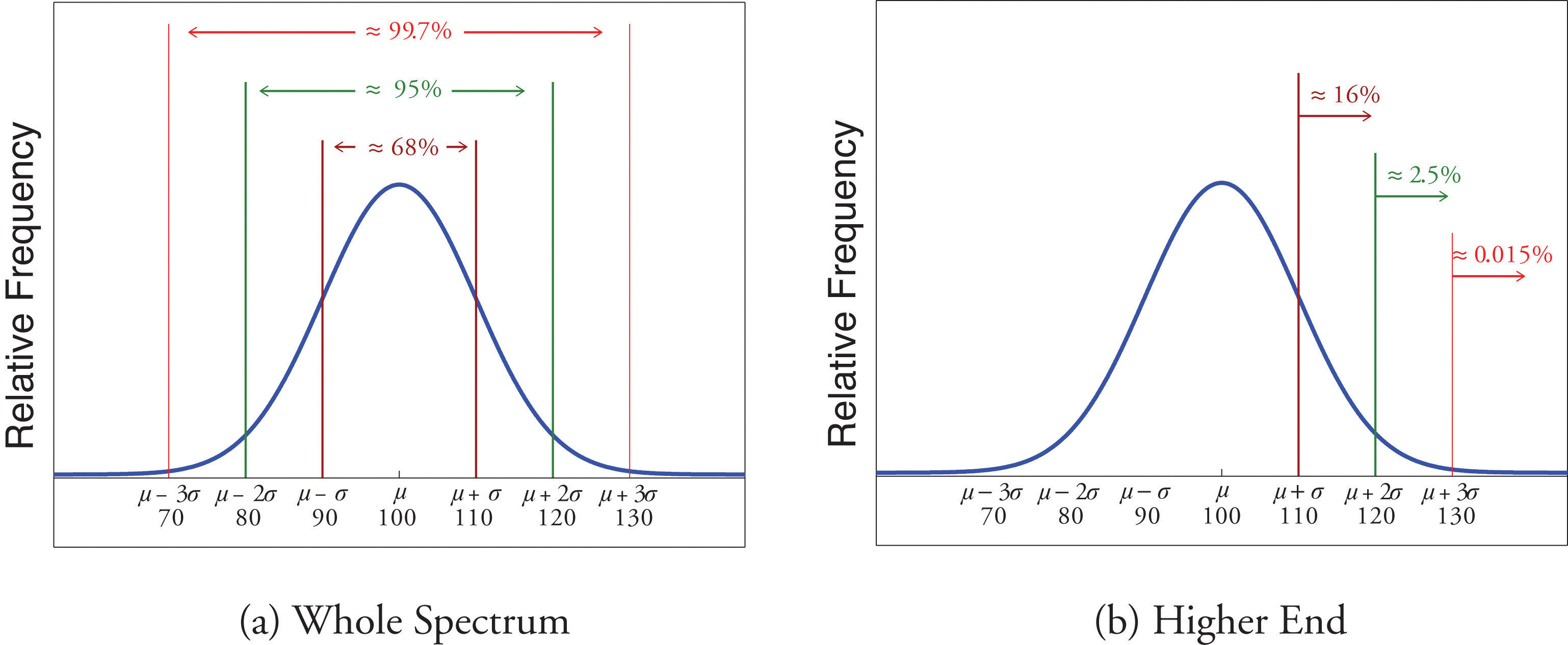
Since 68% of the IQ scores lie within the interval from 90 to 110, it must be the case that 32% lie outside that interval. By symmetry approximately half of that 32%, or 16% of all IQ scores, will lie above 110. If 16% lie above 110, then 84% lie below. We conclude that the IQ score 110 is the 84th percentile.
The same analysis applies to the score 120. Since approximately 95% of all IQ scores lie within the interval form 80 to 120, only 5% lie outside it, and half of them, or 2.5% of all scores, are above 120. The IQ score 120 is thus higher than 97.5% of all IQ scores, and is quite a high score.
By a similar argument, only 15/100 of 1% of all adults, or about one or two in every thousand, would have an IQ score above 130. This fact makes the score 130 extremely high.
The Empirical Rule does not apply to all data sets, only to those that are bell-shaped, and even then is stated in terms of approximations. A result that applies to every data set is known as Chebyshev’s Theorem.
For any numerical data set,
Figure 2.19 "Chebyshev’s Theorem" gives a visual illustration of Chebyshev’s Theorem.
Figure 2.19 Chebyshev’s Theorem
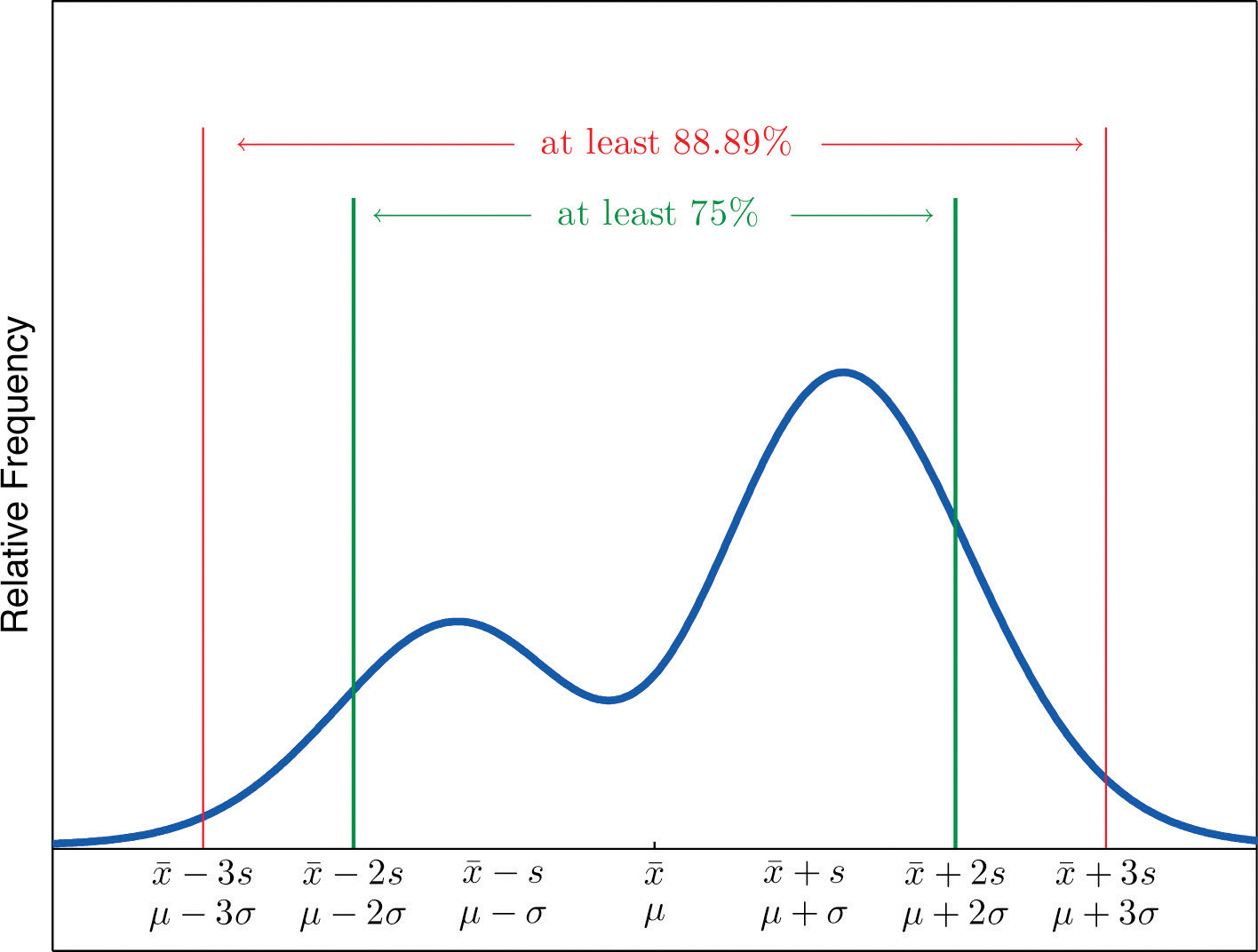
It is important to pay careful attention to the words “at least” at the beginning of each of the three parts. The theorem gives the minimum proportion of the data which must lie within a given number of standard deviations of the mean; the true proportions found within the indicated regions could be greater than what the theorem guarantees.
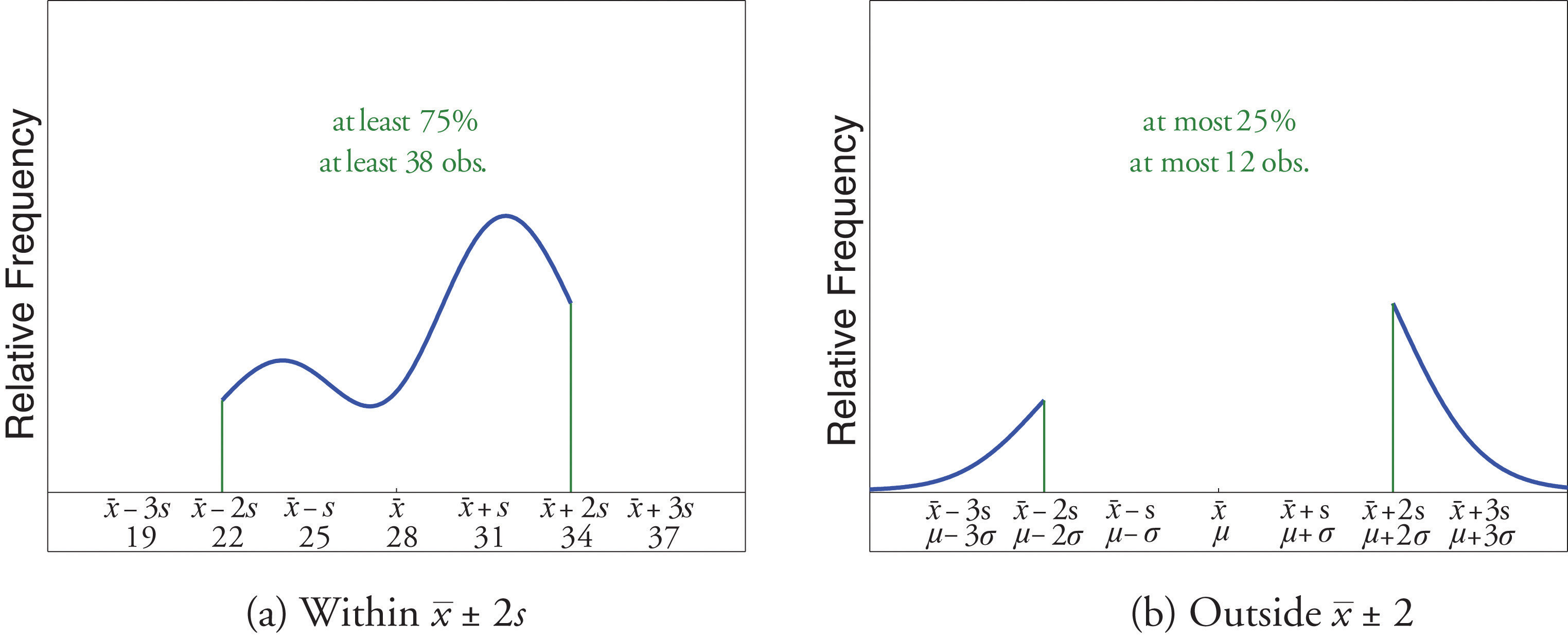
A sample of size n = 50 has mean ˉx=28 and standard deviation s = 3. Without knowing anything else about the sample, what can be said about the number of observations that lie in the interval (22,34)? What can be said about the number of observations that lie outside that interval?
Solution:
The interval (22,34) is the one that is formed by adding and subtracting two standard deviations from the mean. By Chebyshev’s Theorem, at least 3/4 of the data are within this interval. Since 3/4 of 50 is 37.5, this means that at least 37.5 observations are in the interval. But one cannot take a fractional observation, so we conclude that at least 38 observations must lie inside the interval (22,34).
If at least 3/4 of the observations are in the interval, then at most 1/4 of them are outside it. Since 1/4 of 50 is 12.5, at most 12.5 observations are outside the interval. Since again a fraction of an observation is impossible, x (22,34).
The number of vehicles passing through a busy intersection between 8:00 a.m. and 10:00 a.m. was observed and recorded on every weekday morning of the last year. The data set contains n = 251 numbers. The sample mean is ˉx=725 and the sample standard deviation is s = 25. Identify which of the following statements must be true.
Solution:
State the Empirical Rule.
Describe the conditions under which the Empirical Rule may be applied.
State Chebyshev’s Theorem.
Describe the conditions under which Chebyshev’s Theorem may be applied.
A sample data set with a bell-shaped distribution has mean ˉx=6 and standard deviation s = 2. Find the approximate proportion of observations in the data set that lie:
A population data set with a bell-shaped distribution has mean μ = 6 and standard deviation σ = 2. Find the approximate proportion of observations in the data set that lie:
A population data set with a bell-shaped distribution has mean μ = 2 and standard deviation σ = 1.1. Find the approximate proportion of observations in the data set that lie:
A sample data set with a bell-shaped distribution has mean ˉx=2 and standard deviation s = 1.1. Find the approximate proportion of observations in the data set that lie:
A population data set with a bell-shaped distribution and size N = 500 has mean μ = 2 and standard deviation σ = 1.1. Find the approximate number of observations in the data set that lie:
A sample data set with a bell-shaped distribution and size n = 128 has mean ˉx=2 and standard deviation s = 1.1. Find the approximate number of observations in the data set that lie:
A sample data set has mean ˉx=6 and standard deviation s = 2. Find the minimum proportion of observations in the data set that must lie:
A population data set has mean μ = 2 and standard deviation σ = 1.1. Find the minimum proportion of observations in the data set that must lie:
A population data set of size N = 500 has mean μ = 5.2 and standard deviation σ = 1.1. Find the minimum number of observations in the data set that must lie:
A sample data set of size n = 128 has mean ˉx=2 and standard deviation s = 2. Find the minimum number of observations in the data set that must lie:
A sample data set of size n = 30 has mean ˉx=6 and standard deviation s = 2.
A population data set has mean μ = 2 and standard deviation σ = 1.1.
Scores on a final exam taken by 1,200 students have a bell-shaped distribution with mean 72 and standard deviation 9.
Lengths of fish caught by a commercial fishing boat have a bell-shaped distribution with mean 23 inches and standard deviation 1.5 inches.
Hockey pucks used in professional hockey games must weigh between 5.5 and 6 ounces. If the weight of pucks manufactured by a particular process is bell-shaped, has mean 5.75 ounces and standard deviation 0.125 ounce, what proportion of the pucks will be usable in professional games?
Hockey pucks used in professional hockey games must weigh between 5.5 and 6 ounces. If the weight of pucks manufactured by a particular process is bell-shaped and has mean 5.75 ounces, how large can the standard deviation be if 99.7% of the pucks are to be usable in professional games?
Speeds of vehicles on a section of highway have a bell-shaped distribution with mean 60 mph and standard deviation 2.5 mph.
Suppose that, as in the previous exercise, speeds of vehicles on a section of highway have mean 60 mph and standard deviation 2.5 mph, but now the distribution of speeds is unknown.
An instructor announces to the class that the scores on a recent exam had a bell-shaped distribution with mean 75 and standard deviation 5.
The GPAs of all currently registered students at a large university have a bell-shaped distribution with mean 2.7 and standard deviation 0.6. Students with a GPA below 1.5 are placed on academic probation. Approximately what percentage of currently registered students at the university are on academic probation?
Thirty-six students took an exam on which the average was 80 and the standard deviation was 6. A rumor says that five students had scores 61 or below. Can the rumor be true? Why or why not?
For the sample data
x26272829303132f341612621Σx=1,256 and Σx2=35,926.
A sample of size n = 80 has mean 139 and standard deviation 13, but nothing else is known about it.
For the sample data
x12345f8429331Σx=168 and Σx2=300.
For the sample data set
x4748495051f131821Σx=1224 and Σx2=59,940.
See the displayed statement in the text.
See the displayed statement in the text.
0.95.
By Chebyshev’s Theorem at most 1∕9 of the scores can be below 62, so the rumor is impossible.